How To Get the Winning Combination Using Mathematics

Ever fork out ten bucks for a raffle and have some old lady beat you after only investing a quarter? I have and it was ridiculously annoying. Imagine seeing a bucket filled almost entirely with your name deliver the only ticket not yours. Unlikely, right? After all, percentages and randomness determine a raffle, right? WRONG! Certain factors skew the randomness, making the conventional raffle more of a strategy game than a game of chance. Here are some tricks on how to win that basket raffle, explained by mathematics.
Buying Multiple Tickets
But, what if you have multiple tickets? How would your strategy change? What if the bowls are occluded and you can’t see how many entries were in each drawing (or there were sufficiently many that you could not estimate?)
Is it better to put all your eggs (tickets) into one basket (drawing), or distribute them over all the drawings?
Again, let’s make the assumption that you are agnostic as to the prize you win (because, if you only cared about one, and only one, of the prizes you would still put all your tickets into that drawing).
The question comes down to the tradeoff: Does having more ‘skin in the game’ (multiple chances in one drawing), outweigh having multiple attempts at winning prize. Let’s take a look.
- Let’s assume there are N tickets in the lottery before you place in your tickets.
- Let’s assume there are d parallel drawings (competitions to enter).
- Let’s assume that you have t tickets to distribute.
As we have no other information to go on, let’s assume that the existing entries have been uniformly distributed through the drawings. So, before you determine what to do, the N tickets have been spread through the d bowls so that each bowl holds N/d tickets.
Patience Is the Key to Success
Sometimes when the tickets are being drawn, a person merely spins the tickets around and picks one off the top. This inefficient mixing method doesn’t actually mix the tickets at all. It just rotates the tickets in the bucket a few times, which makes whichever one on top more likely to be drawn. So if you’re only going to buy a ticket or two, you might want to wait towards the end of the selling period. You’ll be that much more likely to win the raffle if this is the case.
All eggs in one basket strategy
If you place all t of your tickets into one drawing, the probability of you winning is:
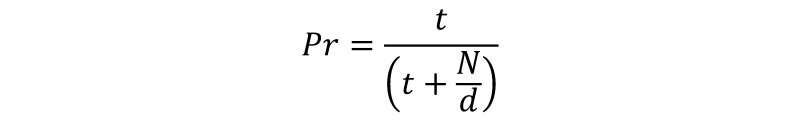
This is a simple calcuation. Before you added your tickets, there were N/d tickets in the bowl. You’ve just added t more, so now the total number of tickets in the bowl is t+(N/d). Out of these, t tickets will cause you to win the prize.
Let’s put some real numbers in there. Let’s imagine there are 1,000 other tickets out there (N=1,000), and that there are five raffles (d=5), and that you have five tickets (t=5).
If you place all your tickets in the same bowl, your chance of winning is 5/(5+(1000/5)) = 5/205 ≈ 2.439%
If you had ten tickets, your odds increase to 10/(10+(1000/5)) = 10/210 ≈ 4.762%, not quite double.
Spread the Love / Disperse Your Resources Strategy
Just like in the above method, inefficient mixing methods can very easily skew randomness. So what if the person drawing the tickets doesn’t thoroughly mix and simply moves clumps around? In that case, your huge stack of tickets might all be on the very bottom. In order to avoid this, try buying periodically throughout the buying window. That way, you know you’ll always have a chance in every raffle regardless of how the tickets are mixed.
Now let’s see what happens if we distribute our tickets through all the drawings.
To calculate the probability of at least one win, we need to find the probability of losing every single drawing and subtract this from 1 (certainty). We need to do this because, with a ‘spread the love’ strategy it’s possible to win more than one of the prizes.
If you have t tickets then distributing these evenly you will be putting t/d additional tickets in each bin which, before you placed in your tickets, held N/d tickets.
You lose a drawing if your ticket is not selected, and this happens N/d times out of (N/d + t/d) times. There are the total of d drawings, so we multiply these probabilities together (logical AND), and this is the dth power:
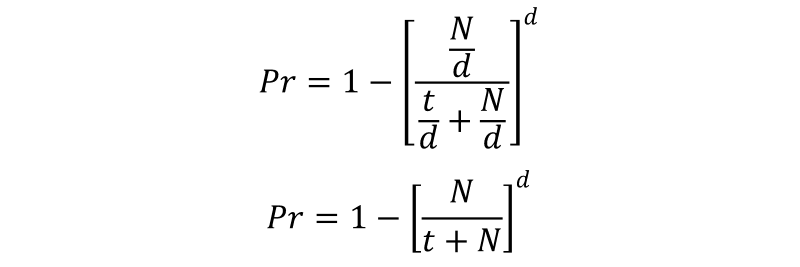
Let’s run the same values from the example above: N=1,000; d=5; t=5
If we place one ticket in each of the five bowls, the odds of winning at least one prize is:
1-(1000/(5+1000))5 = 1-(1000/1005)5 ≈ 2.463%
This is a slightly higher chance than putting all the tickets in one drawing at 2.439% (plus there is also the chance of winning more than one prize!)
In the ten ticket example, if you place two tickets in each of the drawings: N=1,000; d=5; t=10
1-(1000/(10+1000))5 = 1-(1000/1010)5 ≈ 4.853% (cf. 4.762%)
The math is clear – Spread out your tickets*
With a ‘spread the love’ strategy, not only are your chances of winning anything better, you also stand a chance of winning more than one prize.
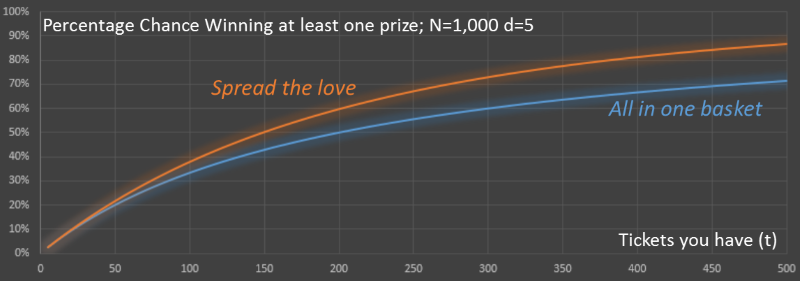
Here is the data in graph format. Below are two curves showing the percentage chance of winning based on the two strategies. For both, the number of other tickets is kept constant at 1,000 and the number of parallel raffles is also kept at five. You can see that the orange line (spreading the love) is always higher than the blue line (putting all tickets in one drawing). Also, remember that by spreading your tickets out there is a chance that you may win more than one prize!
Pick Your Battles
Obviously, a bucket filled to the brim with tickets is going to provide little opportunity for success. If the tickets sold strongly outweigh the cost of the basket, then the raffle was a success for those hosting it, making it a lost cause for you. It’s just like playing the lottery. You’re more likely to spend the total jackpot before you win it, so the practicality in playing is greatly diminished. On the other hand, the cause might make buying a ticket worth it, or maybe just the thrill of gambling. If you want to be a good person or have a good time with it, just try dispersing.
Don’t Leave!
I’ve been around for many raffles in which someone just isn’t there to claim the prize. Don’t expect the drawing to occur before you go. In reality, those tickets aren’t being drawn until the very last minute in most cases. If you’re going to put out the money, at least give yourself a chance to win the raffle.